Page 134 - Statistics for Dummies

118
Part II: Number-Crunching Basics
As shown in the boxplot of the data in Figure 7-7, the ages are skewed right.
The part of the box to the left of the median (representing the younger
actresses) is shorter than the part of the box to the right of the median (rep-
resenting the older actresses). That means the ages of the younger actresses
are closer together than the ages of the older actresses. Figure 7-3 shows the
descriptive statistics of the data and confirms the right skewness: the median
age (33 years) is lower than the mean age (35.69 years).

If one side of the box is longer than the other, it does not mean that side con-
tains more data. In fact, you can’t tell the sample size by looking at a boxplot;
it’s based on percentages, not counts. Each section of the boxplot (the mini-
mum to Q , Q to the median, the median to Q , and Q to the maximum) con-
1
1
3
3
tains 25% of the data no matter what. If one of the sections is longer than
another, it indicates a wider range in the values of data in that section (mean-
ing the data are more spread out). A smaller section of the boxplot indicates
the data are more condensed (closer together).
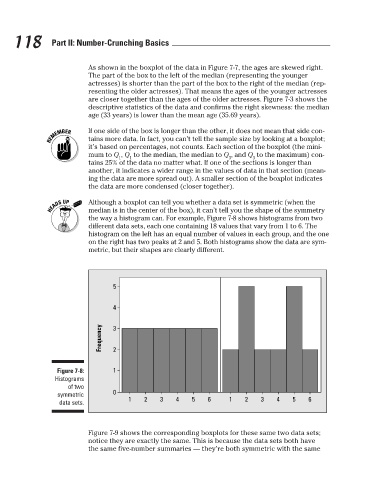
Although a boxplot can tell you whether a data set is symmetric (when the
median is in the center of the box), it can’t tell you the shape of the symmetry
the way a histogram can. For example, Figure 7-8 shows histograms from two
different data sets, each one containing 18 values that vary from 1 to 6. The
histogram on the left has an equal number of values in each group, and the one
on the right has two peaks at 2 and 5. Both histograms show the data are sym-
metric, but their shapes are clearly different.
5
4
Frequency 3 2
Figure 7-8: 1
Histograms
of two
symmetric 0
data sets. 1 2 3 4 5 6 1 2 3 4 5 6

Figure 7-9 shows the corresponding boxplots for these same two data sets;
notice they are exactly the same. This is because the data sets both have
the same five-number summaries — they’re both symmetric with the same

3/25/11 8:16 PM
12_9780470911082-ch07.indd 118 3/25/11 8:16 PM
12_9780470911082-ch07.indd 118