Page 84 - Thermodynamics of Biochemical Reactions

4.11 Tables of Standard Transformed Thermodynamic Properties at 298.15 K 79

Table 4.2 Continued

Reactant PH 5 PH 6 PH 7 PH 8 PH 9
ribose 1 phos - 1320.16 - 1264.30 - 121 1.14 - 11 59.50 - 1108.09
ribose5phos - 1328.24 - 1272.38 - 1219.22 - 1167.58 - 11 16.17
ribulose - 442.44 - 385.36 - 328.28 -271.20 -214.12
serineL - 305.42 - 265.47 - 225.5 1 - 185.55 - 145.60
sorbose - 559.75 -491.26 - 422.76 - 354.26 - 285.77
succinate - 578.32 - 553.73 - 530.64 - 507.79 - 484.95
succinylcoA - 393.33 - 370.32 - 347.47 - 324.63 - 301.80
sucrose -919.00 - 793.43 -667.85 - 542.27 - 416.70
thioredoxinox 0 0 0 0 0
thioredoxinred 33.33 44.70 55.74 64.03 66.35
tryptophaneL 237.50 306.00 374.49 442.99 511.49
t yrosineL -47.85 14.94 77.73 140.51 203.30
ubiquinoneos 2641.49 3155.21 3668.94 4182.66 4696.38
ubiquinonered 2610.27 3135.41 3660.55 4185.69 47 10.8 3
urate -238.66 -221.54 - 204.41 - 187.29 - 170.16
urea - 85.40 -62.51 - 39.74 - 16.90 5.93
uricacid - 239.50 - 216.67 - 193.84 - 171.00 - 148.17
valineL - 35.80 26.99 89.78 152.56 215.35
xylose - 456.99 - 399.91 -342.83 -285.75 - 228.67
xylulose -452.65 - 395.57 - 338.49 -281.41 - 224.33

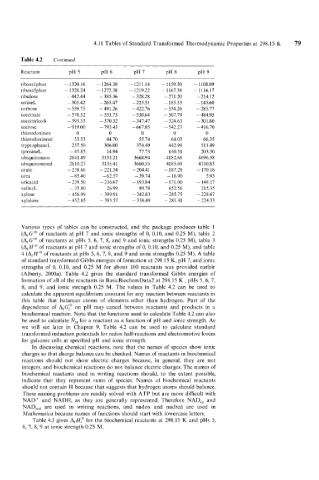
Various types of tables can be constructed, and the package produces table 1
(A,G" of reactants at pH 7 and ionic strengths of 0, 0.10, and 0.25 M), table 2
(AfG" of reactants at pHs 5, 6, 7, 8, and 9 and ionic strengths 0.25 M), table 3
(AfH'O of reactants at pH 7 and ionic strengths of 0, 0.10, and 0.25 M), and table
4 (AfH'' of reactants at pHs 5, 6, 7, 8, and 9 and ionic strengths 0.25 M). A table
of standard transformed Gibbs energies of formation at 298.15 K, pH 7, and ionic
strengths of 0, 0.10, and 0.25 M for about 100 reactants was provided earleir
(Alberty, 2000a). Table 4.2 gives the standard transformed Gibbs energies of
formation of all of the reactants in BasicBiochemData2 at 298.15 K , pHs 5, 6, 7,
8, and 9, and ionic strength 0.25 M. The values in Table 4.2 can be used to
calculate the apparent equilibrium constant for any reaction between reactants in
this table that balances atoms of elements other than hydrogen. Part of the
dependence of AfGIo on pH may cancel between reactants and products in a
biochemical reaction. Note that the functions used to calculate Table 4.2 can also
be used to calculate NH for a reactant as a function of pH and ionic strength. As
we will see later in Chapter 9, Table 4.2 can be used to calculate standard
transformed reduction potentials for redox half-reactions and electromotive forces
for galvanic cells at specified pH and ionic strength.
In discussing chemical reactions, note that the names of species show ionic
charges so that charge balance can be checked. Names of reactants in biochemical
reactions should not show electric charges because, in general, they are not
integers, and biochemical reactions do not balance electric charges. The names of
biochemical reactants used in writing reactions should, to the extent possible,
indicate that they represent sums of species. Names of biochemical reactants
should not contain H because that suggests that hydrogen atoms should balance.
These naming problems are readily solved with ATP but are more difficult with
NAD and NADH, as they are generally represented. Therefore NAD,, and
+
NAD,,, are used in writing reactions, and nadox and nadred are used in
Mathernatica because names of functions should start with lowercase letters.
Table 4.3 gives AfHi0 for the biochemical reactants at 298.15 K and pHs 5,
6, 7, 8, 9 at ionic strength 0.25 M.