Page 189 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
QC: —/—
P1: KVU/KXT
P2: KVU/KXT
June 22, 2007
AT029-Manual-v7.cls
AT029-04
21:30
AT029-Manual
4. CHARACTERIZATION OF RESERVOIR FLUIDS AND CRUDE OILS 169
following relation for the average molecular weight of the
Carbon Number, C
N
SCN group n:
0 20 40 60 80
0.01 M 7+ − η η
M av,n =− exp
x m,n M 7+ − η
M + M +
0.008 n n
1 × M 7+ − η + 1 exp − M 7+ − η
M n − + 1 exp − M n −

PDF, F 0.006 2 M 7+ − η M 7+ − η
(4.48)
−
where M av,n is the average molecular weight of SCN group n.
0.004 Equations (4.47) and (4.48) can also be applied to any group
2.5
with known lower and upper molecular weight boundaries in
aC 7+ fraction that follows an exponential distribution.
0.002 3
Example 4.5—Show that distribution model expressed by
0 Eq. (4.46) leads to Eq. (4.27) for exponential distribution of
SCN groups.
0 200 400 600 800 1000 1200
Molecular Weight, M
Solution—Equation (4.46) can be written in the following
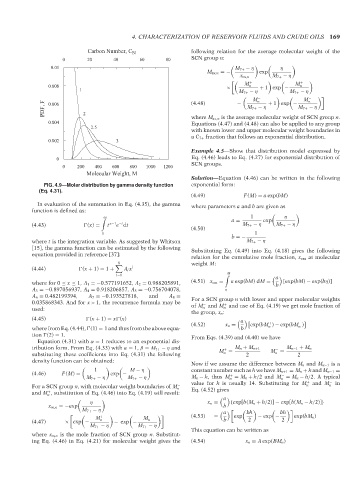
FIG. 4.9—Molar distribution by gamma density function exponential form:
(Eq. 4.31).
(4.49) F(M) = a exp(bM)
In evaluation of the summation in Eq. (4.35), the gamma where parameters a and b are given as
function is defined as:
1 η
∞
a = exp
e dt
(4.43) (x) = t x−1 −t M 7+ − η M 7+ − η
(4.50)
0 1
b =−
where t is the integration variable. As suggested by Whitson M 7+ − η
[15], the gamma function can be estimated by the following Substituting Eq. (4.49) into Eq. (4.18) gives the following
equation provided in reference [37]:
relation for the cumulative mole fraction, x cm at molecular
weight M:
8
(4.44) (x + 1) = 1 + A i x i
M
i=1
a

where for 0 ≤ x ≤ 1, A 1 =−0.577191652, A 2 = 0.988205891, (4.51) x cm = a exp(bM)dM = b [exp(bM) − exp(bη)]
A 3 =−0.897056937, A 4 = 0.918206857, A 5 =−0.756704078, η
A 6 = 0.482199394, A 7 =−0.193527818, and A 8 =
0.035868343. And for x > 1, the recurrence formula may be For a SCN group n with lower and upper molecular weights
−
+
n
n
used: of M and M and use of Eq. (4.19) we get mole fraction of
the group, x n :
(4.45) (x + 1) = x (x)
(4.52) x n = a exp(bM ) − exp(bM )
−
+
n
n
where from Eq. (4.44), (1) = 1 and thus from the above equa- b
tion (2) = 1. From Eqs. (4.39) and (4.40) we have
Equation (4.31) with α = 1 reduces to an exponential dis-
tribution form. From Eq. (4.33) with α = 1, β = M 7+ − η and M n + M n+1 M n−1 + M n
+
−
M = M =
n
n
substituting these coefficients into Eq. (4.31) the following 2 2
density function can be obtained:
Now if we assume the difference between M n and M n−1 is a
1 M − η constant number such as hwe have M n+1 = M n + hand M n−1 =

(4.46) F(M) = exp −
−
+
M 7+ − η M 7+ − η M n − h, thus M = M n + h/2 and M = M n − h/2. A typical
n
n
value for h is usually 14. Substituting for M n + and M n − in
For a SCN group n, with molecular weight boundaries of M −
n Eq. (4.52) gives
and M , substitution of Eq. (4.46) into Eq. (4.19) will result:
+
n
a

η x n = {exp[b(M n + h/2)] − exp[b(M n − h/2)]}
x m,n =−exp b
M 7+ − η
bh bh
a
M + M −
(4.53) = exp − exp − exp(bM n )
(4.47) × exp − n − exp − n b 2 2
M 7+ − η M 7+ − η
This equation can be written as
where x m,n is the mole fraction of SCN group n. Substitut-
ing Eq. (4.46) in Eq. (4.21) for molecular weight gives the (4.54) x n = A exp(BM n )
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT