Page 331 - Analysis, Synthesis and Design of Chemical Processes, Third Edition

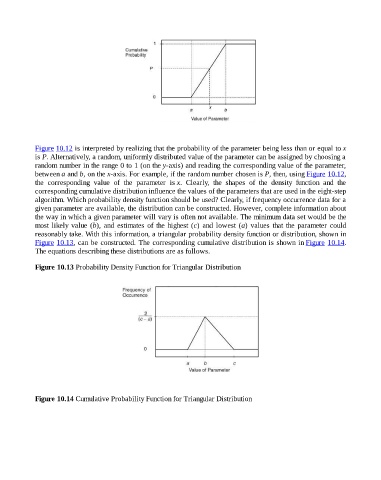
Figure 10.12 is interpreted by realizing that the probability of the parameter being less than or equal to x
is P. Alternatively, a random, uniformly distributed value of the parameter can be assigned by choosing a
random number in the range 0 to 1 (on the y-axis) and reading the corresponding value of the parameter,
between a and b, on the x-axis. For example, if the random number chosen is P, then, using Figure 10.12,
the corresponding value of the parameter is x. Clearly, the shapes of the density function and the

corresponding cumulative distribution influence the values of the parameters that are used in the eight-step
algorithm. Which probability density function should be used? Clearly, if frequency occurrence data for a
given parameter are available, the distribution can be constructed. However, complete information about
the way in which a given parameter will vary is often not available. The minimum data set would be the
most likely value (b), and estimates of the highest (c) and lowest (a) values that the parameter could
reasonably take. With this information, a triangular probability density function or distribution, shown in
Figure 10.13, can be constructed. The corresponding cumulative distribution is shown in Figure 10.14.
The equations describing these distributions are as follows.

Figure 10.13 Probability Density Function for Triangular Distribution

Figure 10.14 Cumulative Probability Function for Triangular Distribution