Page 332 - Analysis, Synthesis and Design of Chemical Processes, Third Edition

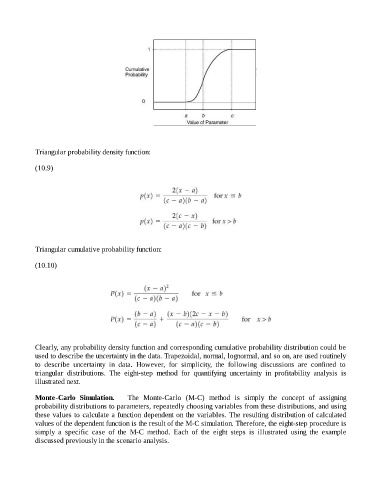
Triangular probability density function:

(10.9)

Triangular cumulative probability function:

(10.10)

Clearly, any probability density function and corresponding cumulative probability distribution could be
used to describe the uncertainty in the data. Trapezoidal, normal, lognormal, and so on, are used routinely
to describe uncertainty in data. However, for simplicity, the following discussions are confined to
triangular distributions. The eight-step method for quantifying uncertainty in profitability analysis is

illustrated next.

Monte-Carlo Simulation. The Monte-Carlo (M-C) method is simply the concept of assigning
probability distributions to parameters, repeatedly choosing variables from these distributions, and using

these values to calculate a function dependent on the variables. The resulting distribution of calculated
values of the dependent function is the result of the M-C simulation. Therefore, the eight-step procedure is
simply a specific case of the M-C method. Each of the eight steps is illustrated using the example
discussed previously in the scenario analysis.