Page 236 - Applied statistics and probability for engineers

214 Chapter 6/Descriptive Statistics

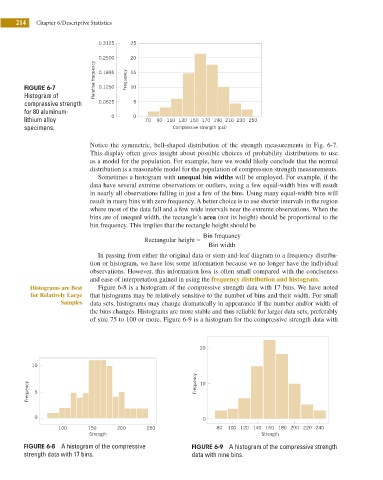
0.3125 25
0.2500 20
Relative frequency 0.1895 Frequency 15

FIGURE 6-7 0.1250 10
Histogram of
compressive strength 0.0625 5
for 80 aluminum-
0 0
lithium alloy 70 90 110 130 150 170 190 210 230 250
specimens. Compressive strength (psi)

Notice the symmetric, bell-shaped distribution of the strength measurements in Fig. 6-7.
This display often gives insight about possible choices of probability distributions to use
as a model for the population. For example, here we would likely conclude that the normal
distribution is a reasonable model for the population of compression strength measurements.
Sometimes a histogram with unequal bin widths will be employed. For example, if the
data have several extreme observations or outliers, using a few equal-width bins will result
in nearly all observations falling in just a few of the bins. Using many equal-width bins will
result in many bins with zero frequency. A better choice is to use shorter intervals in the region
where most of the data fall and a few wide intervals near the extreme observations. When the
bins are of unequal width, the rectangle’s area (not its height) should be proportional to the
bin frequency. This implies that the rectangle height should be
Rectangular height = Bin frequancy
Bin width
In passing from either the original data or stem-and-leaf diagram to a frequency distribu-
tion or histogram, we have lost some information because we no longer have the individual
observations. However, this information loss is often small compared with the conciseness
and ease of interpretation gained in using the frequency distribution and histogram.
Histograms are Best Figure 6-8 is a histogram of the compressive strength data with 17 bins. We have noted
for Relatively Large that histograms may be relatively sensitive to the number of bins and their width. For small
Samples data sets, histograms may change dramatically in appearance if the number and/or width of
the bins changes. Histograms are more stable and thus reliable for larger data sets, preferably
of size 75 to 100 or more. Figure 6-9 is a histogram for the compressive strength data with

20

10

Frequency 5 Frequency 10

0 0
100 150 200 250 80 100 120 140 160 180 200 220 240
Strength Strength
FIGURE 6-8 A histogram of the compressive FIGURE 6-9 A histogram of the compressive strength
strength data with 17 bins. data with nine bins.