Page 479 - Engineering Digital Design

10.7 THE D FLIP-FLOPS: GENERAL 449

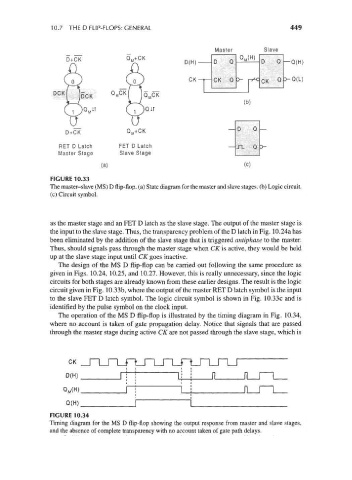
Master Slave
D+CK -„.-.- D(H)
D Q -^- D Q -Q(H)
CK CK Q , fCK Q D-Q(L)

(b)

D + CK
RET D Latch FET D Latch
Master Stage Slave Stage

(a) (c)
FIGURE 10.33
The master-slave (MS) D flip-flop, (a) State diagram for the master and slave stages, (b) Logic circuit,
(c) Circuit symbol.

as the master stage and an FET D latch as the slave stage. The output of the master stage is
the input to the slave stage. Thus, the transparency problem of the D latch in Fig. 10.24a has
been eliminated by the addition of the slave stage that is triggered antiphase to the master.
Thus, should signals pass through the master stage when CK is active, they would be held
up at the slave stage input until CK goes inactive.
The design of the MS D flip-flop can be carried out following the same procedure as
given in Figs. 10.24, 10.25, and 10.27. However, this is really unnecessary, since the logic
circuits for both stages are already known from these earlier designs. The result is the logic
circuit given in Fig. 10.33b, where the output of the master RET D latch symbol is the input
to the slave FET D latch symbol. The logic circuit symbol is shown in Fig. 10.33c and is
identified by the pulse symbol on the clock input.
The operation of the MS D flip-flop is illustrated by the timing diagram in Fig. 10.34,
where no account is taken of gate propagation delay. Notice that signals that are passed
through the master stage during active CK are not passed through the slave stage, which is

CK

D(H)

Q(H)

FIGURE 10.34
Timing diagram for the MS D flip-flop showing the output response from master and slave stages,
and the absence of complete transparency with no account taken of gate path delays.