Page 764 - Engineering Digital Design

730 CHAPTER 14 / ASYNCHRONOUS STATE MACHINE DESIGN AND ANALYSIS

S(H)

T(H)

Y 3(H)

y^H)

y 0(H)
0111 1111
b d
P(H)

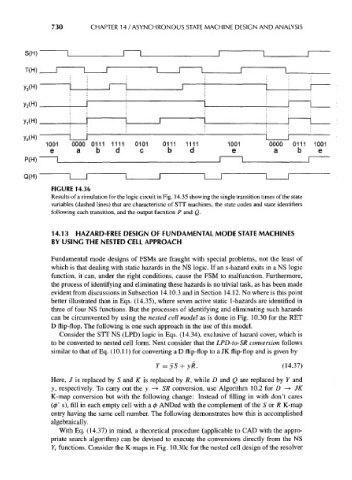
FIGURE 14.36
Results of a simulation for the logic circuit in Fig. 14.35 showing the single transition times of the state
variables (dashed lines) that are characteristic of STT machines, the state codes and state identifiers
following each transition, and the output fucntion P and Q.

14.13 HAZARD-FREE DESIGN OF FUNDAMENTAL MODE STATE MACHINES
BY USING THE NESTED CELL APPROACH

Fundamental mode designs of FSMs are fraught with special problems, not the least of
which is that dealing with static hazards in the NS logic. If an s-hazard exits in a NS logic
function, it can, under the right conditions, cause the FSM to malfunction. Furthermore,
the process of identifying and eliminating these hazards is no trivial task, as has been made
evident from discussions in Subsection 14.10.3 and in Section 14.12. No where is this point
better illustrated than in Eqs. (14.35), where seven active static 1-hazards are identified in
three of four NS functions. But the processes of identifying and eliminating such hazards
can be circumvented by using the nested cell model as is done in Fig. 10.30 for the RET
D flip-flop. The following is one such approach in the use of this model.
Consider the STT NS (LPD) logic in Eqs. (14.34), exclusive of hazard cover, which is
to be converted to nested cell form. Next consider that the LPD-to-SR conversion follows
similar to that of Eq. (10.11) for converting a D flip-flop to a JK flip-flop and is given by
Y = yS + yR. (14.37)

Here, J is replaced by S and K is replaced by R, while D and Q are replaced by Y and
y, respectively. To carry out the y —> SR conversion, use Algorithm 10.2 for D —> JK
K-map conversion but with the following change: Instead of filling in with don't cares
(0' s), fill in each empty cell with a 0 ANDed with the complement of the S or R K-map
entry having the same cell number. The following demonstrates how this is accomplished
algebraically.
With Eq. (14.37) in mind, a theoretical procedure (applicable to CAD with the appro-
priate search algorithm) can be devised to execute the conversions directly from the NS
YJ functions. Consider the K-maps in Fig. 10.30c for the nested cell design of the resolver