Page 87 - Finite Element Modeling and Simulations with ANSYS Workbench

72 Finite Element Modeling and Simulation with ANSYS Workbench

(a) (b)
1 0.15

0.1
0.5
0.05

0 0
0 0.5 1 0 0.5 1
N (x) N (x)
1
2
(c) (d)
1 0
–0.05
0.5
–0.1

0 –0.15
0 0.5 1 0 0.5 1
N (x) N (x)
3
4
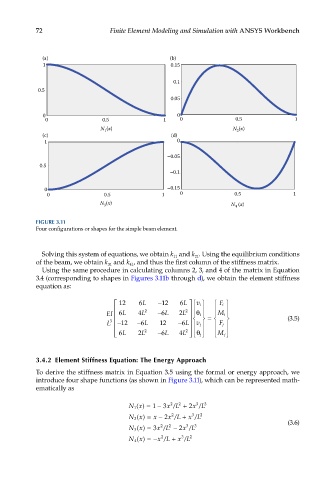
FIGURE 3.11
Four configurations or shapes for the simple beam element.

Solving this system of equations, we obtain k and k . Using the equilibrium conditions
21
11
of the beam, we obtain k and k , and thus the first column of the stiffness matrix.
31
41
Using the same procedure in calculating columns 2, 3, and 4 of the matrix in Equation
3.4 (corresponding to shapes in Figures 3.11b through d), we obtain the element stiffness
equation as:
v

 12 6 L − 12 6 L  v i   F i 


i θ
EI 6 L 4 L 2 − 6 L 2 L 2    M i  (3.5)
 



  = 
L  − 12 − 6 L 12 − 6 L v j  F j 
3

 
2 
 2 L    
j θ
 6 L 2 L − 6 L 4    M j 
3.4.2 Element Stiffness Equation: The Energy Approach
To derive the stiffness matrix in Equation 3.5 using the formal or energy approach, we
introduce four shape functions (as shown in Figure 3.11), which can be represented math-
ematically as
2
Nx() = 1 − 3 xL + 2 xL 3
3
2
/
/
1
3
2
Nx() = x − 2 x L + x L 2
/
/
2
2
Nx() = 3 xL − 2 xL 3 3 (3.6)
3
2
/
/
3
Nx() =− xL + xL 2
3
2
/
/
4