Page 155 -

4.3 Theoretical Analysis II – Fluid Dynamics 145
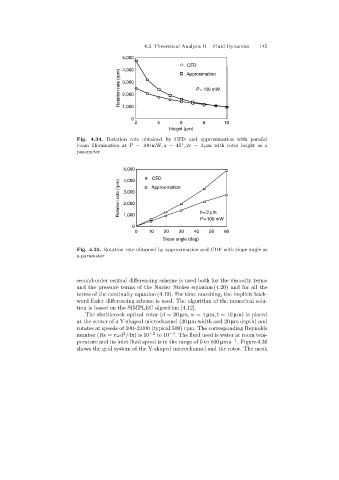
5,000
CFD
4,000
Rotation rate (rpm) 3,000 P=100 mW
Approximation

2,000

1,000

0
2 4 6 8 10
Height (mm)
Fig. 4.34. Rotation rate obtained by CFD and approximation with parallel
◦
beam illumination at P = 100 mW,a =45 , 2r =3 µm with rotor height as a
parameter

5,000 CFD
Rotation rate (rpm) 3,000 Approximation
4,000

2,000
h=3 mm
1,000
P=100 mW
0
0 10 20 30 40 50 60
Slope angle (deg)
Fig. 4.35. Rotation rate obtained by approximation and CDF with slope angle as
a parameter

second-order central differencingscheme is used both for the viscosity terms
and the pressure terms of the Navier–Stokes equation (4.20) and for all the
terms of the continuity equation (4.19). For time marching, the implicit back-
ward Euler differencingscheme is used. The algorithm of the numerical solu-
tion is based on the SIMPLEC algorithm [4.12].
The shuttlecock optical rotor (d =20 µm,w =4 µm,t =10 µm) is placed
at the center of a Y-shaped microchannel (30 µm width and 20 µm depth) and
rotates at speeds of 100–2,000 (typical 500) rpm. The correspondingReynolds
2
number (Re = rωd /4π)is10 −2 to 10 −4 . The fluid used is water at room tem-
perature and its inlet fluid speed is in the range of 0 to 100 µms −1 . Figure 4.36
shows the grid system of the Y-shaped microchannel and the rotor. The mesh