Page 149 - Schaum's Outline of Theory and Problems of Advanced Calculus

140 PARTIAL DERIVATIVES [CHAP. 6

Similarly, x y ¼ 2becomes ðu þ vÞ ðu vÞ¼ 2or v ¼ 1, which is a line (shown dashed) in the
uv plane. In like manner, y ¼ 0becomes u v ¼ 0or u ¼ v, which is a line shown heavy in the uv
plane. Then the required region is bounded by u ¼ 3, v ¼ 1 and u ¼ v, and is shown shaded in Fig. 6-
9(b).
@ @

@x @x

ðu þ vÞ ðu þ vÞ 1
@u @u @v 1

@ðx; yÞ @v
¼ 2
ðbÞ ¼ ¼ ¼
@y @ @

@ðu; vÞ 1 1
@y
@u @v @u @v
ðu vÞ ðu vÞ
(c) The area of triangular region r is 4, whereas the area of triangular region r is 2. Hence, the ratio is
0
4=2 ¼ 2, agreeing with the value of the Jacobian in (b). Since the Jacobian is constant in this case, the
areas of any regions r in the xy plane are twice the areas of corresponding mapped regions r in the uv
0
plane.
2
2
2
2
2
2
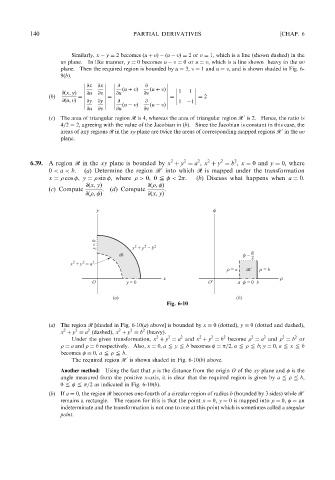
6.39. A region r in the xy plane is bounded by x þ y ¼ a , x þ y ¼ b , x ¼ 0 and y ¼ 0, where
0 < a < b. (a) Determine the region r into which r is mapped under the transformation
0
x ¼ cos , y ¼ sin , where > 0, 0 @ < 2 . (b) Discuss what happens when a ¼ 0.
(c) Compute @ðx; yÞ . (d) Compute @ð ; Þ .
@ð ; Þ @ðx; yÞ

Fig. 6-10

(a) The region r [shaded in Fig. 6-10(a) above] is bounded by x ¼ 0(dotted), y ¼ 0(dotted and dashed),
2
2
2
2
2
2
x þ y ¼ a (dashed), x þ y ¼ b (heavy).
2
2
2
2
2
2
2
2
2
2
Under the given transformation, x þ y ¼ a and x þ y ¼ b become ¼ a and ¼ b or
¼ a and ¼ b respectively. Also, x ¼ 0, a @ y @ b becomes ¼ =2, a @ @ b; y ¼ 0, a @ x @ b
becomes ¼ 0, a @ @ b.
The required region r is shown shaded in Fig. 6-10(b) above.
0
Another method: Using the fact that is the distance from the origin O of the xy plane and is the
angle measured from the positive x-axis, it is clear that the required region is given by a @ @ b,
0 @ @ =2as indicated in Fig. 6-10(b).
(b)If a ¼ 0, the region r becomes one-fourth of a circular region of radius b (bounded by 3 sides) while r 0
remains a rectangle. The reason for this is that the point x ¼ 0, y ¼ 0is mapped into ¼ 0, ¼ an
indeterminate and the transformation is not one to one at this point which is sometimes called a singular
point.