Page 122 - Separation process principles 2

F-

3.3 One-Dimensional, Steady-State and Unsteady-State, Molecular Diffusion through Stationary Media 87

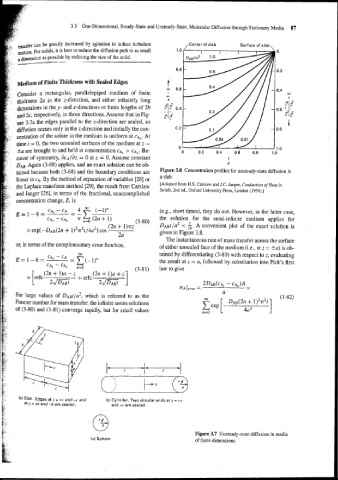
transfer can be greatly increased by agitation to induce turbulent /Center of slab Surface of slab,
?i
motion For solids, it is best to reduce the diffusion path to as small
a dimension as possible by reducing the size of the solid.

Medium of Finite Thickness with Sealed Edges
consider a rectangular, parallelepiped medium of finite
thickness 2a in the z-direction, and either infinitely long
dimensions in the y- and x-directions or finite lengths of 2b
and 2c, respectively, in those directions. Assume that in Fig-
ure 3.7a the edges parallel to the z-direction are sealed, so
diffusion occurs only in the z-direction and initially the con-
centration of the solute in the medium is uniform at CA~. At
time t = 0, the two unsealed surfaces of the medium at =
20 are brought to and held at concentration cAS > cAo. Be-
cause of symmetry, &A/& = 0 at z = 0. Assume constant -
L
D~ Again (3-68) applies, and an exact solution can be ob- a
tained because both (3-68) and the boundary conditions are Figure 3.8 Concentration profiles for unsteady-state diffusion in
a slab.
linear in CA. By the method of separation of variables [28] or
[Adapted from H.S. Carslaw and J.C. Jaeger, Conduction ofHeat in
the Laplace transform method [29], the result from Carslaw
Solids, 2nd ed., Oxford University Press, London (1959).]
and Jaeger [26], in terms of the fractional, unaccomplished
concentration change, E, is
CA>-CA =-c--
E=l-0= 4 00 (e.g., short times), they do not. However, in the latter case,
CA,-CA, nnn=(2n+1) the solution for the semi-infinite medium applies for
DAB~/U~ < h. A convenient plot of the exact solution is
(2n + 1)nz (3-80)
+
X e~p[-D~~(2n I)~IT~~/~U~] given in Figure 3.8.
COS
2a
The instantaneous rate of mass transfer across the surface
or, in terms of the complementary error function,
of either unsealed face of the medium (i.e., at z = +a) is ob-
CO tained by differentiating (3-80) with respect to z, evaluating
CAS - CA
E=~-B= = C(-l)" the result at z = a, followed by substitution into Fick's first
CAs - CAo n=~ (3-81) law to give
(2n + l)a - z (2n + l)a + z
x [edc + erfc I
-
2miz 2- ~DAB(CA$ CAJA
nAIz=a =
a
For large values of ~~~t/a~, which is referred to as the (3-82)
Fourier number for mass transfer, the infinite series solutions 2 exp [ DAB(^^ + 1)'n2t]
-
of (3-80) and (3-81) converge rapidly, but for small values
n=O 4a2

(a) Slab. Edges at x = tc and -C and (b) Cylinder. Two circular ends at x = tc
=
at~ +b and -b are sealed. and -c are sealed.

Figure 3.7 Unsteady-state diffusion in media
(c) Sphere
of finite dimensions.