Page 123 - Separation process principles 2

88 Chapter 3 Mass Transfer and Diffusion

We can also determine the total number of moles transferred This equation is plotted in Figure 3.9. It is important to note
across either unsealed face by integrating (3-82) with respect that concentrations are in mass of solute per mass of dry
to time. Thus, solid or mass of solute/volume. This assumes that during dif-
fusion the solid does not shrink or expand so that the mass of
dry solid per unit volume of wet solid will remain constant.
1 { [ DAB(^^ -k l)'Ti2t] 1 Then, we can substitute a concentration in terms of mass or
moles of solute per mass of dry solid, i.e., the moisture con-
1 - exp -
C (2n + 112 4a2 tent on the dry basis.
n=O
When the edges of the slab in Figure 3.7a are not sealed,
(3-83)
the method of Newnian [31] can be used with (3-69) to
In addition, the average concentration of the solute in the determine concentration changes within the slab. In this
medium, CA,,,, as a function of time, can be obtained in the method, E or Eavg is given in terms of the E values from the
solution of (3-68) for each of the coordinate directions by
case of a slab from:

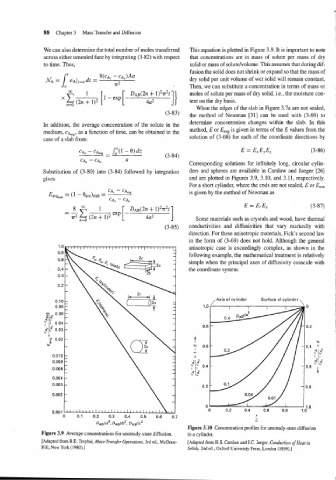
Corresponding solutions for infinitely long, circular cylin-
Substitution of (3-80) into (3-84) followed by integration ders and spheres are available in Carslaw and Jaeger [26]
gives and are plotted in Figures 3.9, 3.10, and 3.11, respectively.
For a short cylinder, where the ends are not sealed, E or Eav,
is given by the method of Newman as

Some materials such as crystals and wood, have thermal
conductivities and diffusivities that vary markedly with
direction. For these anisotropic materials, Fick's second law
in the form of (3-69) does not hold. Although the general
anisotropic case is exceedingly complex, as shown in the
following example, the mathematical treatment is relatively
simple when the principal axes of diffusivity coincide with
the coordinate system.

,Axis of cylinder Surface of cylinder,

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
0
DABt/a2, DABt/b2, D~~~/c~
Figure 3.10 Concentration profiles for unsteady-state diffusion
Figure 3.9 Average concentrations for unsteady-state diffusion. in a cylinder.
[Adapted from R.E. Treybal, Mass-Transfer Operations, 3rd ed., McGraw- [Adapted from H.S. Carslaw and J.C. Jaeger, Conduction of Heat in
Hill, New York (1980).] Solids, 2nd ed., Oxford University Press, London (1959).]