Page 203 - Sustainability in the Process Industry Integration and Optimization

180 Cha p te r E i g h t

case study from a real-life multipurpose batch facility is presented
next.

Example 8.3: Optimal Scheduling
The case study is taken from a multinational pharmaceuticals facility that
produces lotions, shampoos, conditioners, and various creams. The problem
features nonintermediate storage policy (NIS), and the processes involve
mixing and packaging. Mixing occurs in four mixing vessels (V1, V2, V3, and
V4), and packaging occurs in three packing lines (P1, P2, and P3). Because the
stirrers in mixing vessels are of different designs, mixing times vary according
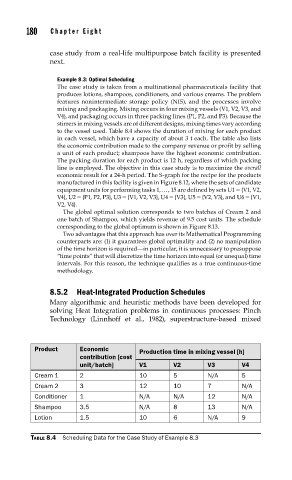
to the vessel used. Table 8.4 shows the duration of mixing for each product
in each vessel, which have a capacity of about 3 t each. The table also lists
the economic contribution made to the company revenue or profit by selling
a unit of each product; shampoos have the highest economic contribution.
The packing duration for each product is 12 h, regardless of which packing
line is employed. The objective in this case study is to maximize the overall
economic result for a 24-h period. The S-graph for the recipe for the products
manufactured in this facility is given in Figure 8.12, where the sets of candidate
equipment units for performing tasks 1, . . . , 15 are defined by sets U1 = {V1, V2,
V4}, U2 = {P1, P2, P3}, U3 = {V1, V2, V3}, U4 = {V3}, U5 = {V2, V3}, and U6 = {V1,
V2, V4}.
The global optimal solution corresponds to two batches of Cream 2 and
one batch of Shampoo, which yields revenue of 9.5 cost units. The schedule
corresponding to the global optimum is shown in Figure 8.13.
Two advantages that this approach has over its Mathematical Programming
counterparts are: (1) it guarantees global optimality and (2) no manipulation
of the time horizon is required—in particular, it is unnecessary to presuppose
“time points” that will discretize the time horizon into equal (or unequal) time
intervals. For this reason, the technique qualifies as a true continuous-time
methodology.

8.5.2 Heat-Integrated Production Schedules
Many algorithmic and heuristic methods have been developed for
solving Heat Integration problems in continuous processes: Pinch
Technology (Linnhoff et al., 1982), superstructure-based mixed

Product Economic Production time in mixing vessel [h]
contribution [cost
unit/batch] V1 V2 V3 V4
Cream 1 2 10 5 N/A 5
Cream 2 3 12 10 7 N/A
Conditioner 1 N/A N/A 12 N/A
Shampoo 3.5 N/A 8 13 N/A
Lotion 1.5 10 6 N/A 9

TABLE 8.4 Scheduling Data for the Case Study of Example 8.3